Graeme Obree's Beastie: The Lure of the Linear Pedal Drive

This post was inspired by Graeme Obree, two time world hour record holder on modified upright bikes and who, at the age of 48, rode his Beastie streamlined prone bicycle into the record books last September. Obree was attempting to break the flying 200m sprint for human-powered vehicles which stands near 83mph. At 56.6mph, Obree came up a bit short. Nonetheless, he did break the record for a streamlined vehicle using a prone rider position, and more significantly, in my opinion, he broke the record for a vehicle using a non-circular pedaling motion.

The two pictures below show a kinematic model of the Beastie's drive mechanism and an enlargement of the resulting pedal path. The path is an elongated ellipse whose major axis is tilted slightly downward front to back.

In the pictures above the cranks rotate in a clockwise direction and the pedals move in a counter-clockwise direction around the ellipse.

Obree bested the existing record for a linear-drive and prone-posture streamliner held by Richard Byrne on Steve Ball’s Dragonfly of 54.9mph. The Dragonfly used both arms and legs moving in straight paths for propulsion. The picture below is from Human Powered Vehicles by Abbott & Wilson.

For the purposes of the following discussion, I consider linear motion to include pedals moving in a straight  line, pedals moving in large arc over a small portion of a circle, and numerous curves generated by four-bar linkages having paths that are significantly longer (in the leg-extension direction) than they are wide. These coupler curves could be egg shaped, elliptical, figure-eight shaped among others. In the case of the Beastie, the pedal path is an elongated ellipse.

When someone of a technical bent takes a close look at the bicycle for the first time, they invariably comment that there has to be a more efficient means for the body to generate mechanical power than circular pedaling. Since a runner’s feet don’t go in circles, it makes no sense that feet going in circles on a bicycle are either natural or efficient. More often than not, the conclusion is that feet moving in a near-linear path would be a significant improvement.

The drive mechanisms that will be discussed here fall into two broad categories, oscillating treadles and constant-torque treadles

Oscillating treadles consist of an input link permanently connected to an output crank through an intermediate link. When the output crank moves continuously, the output link moves back and forth between its extreme positions or oscillates. For a constant crank speed, the speed of the input link varies over the cycle and often comes to a complete stop at the limits of travel. By its very nature, one important characteristic of the oscillating treadle is that one cycle of the input link results in only one rotation of the output crank. Some form of gearing is usually required between the crank and the wheel. These systems work best with fixed gearing so that the vehicle motion carries the pedals through their motion-dead spots.

 The crank slider (the core of every IC engine) is an oscillating treadle. The mechanism used in the Beastie was a offset-crank slider where the slider track is not lined up with the crank pivot. In addition, the pedal is located above the connecting rod. This produces a relatively horizontal-flattened ellipse located above the crank center, which accommodated the rider being located above the crank center.

Because friction associated with the slider can waste energy, a rocker link often replaces the slider for mechanism used for human power generation. The connecting rod moves through a short segment of a large arc instead of a straight path.

When used by Kirkpatrick McMillan in the mid 1800’s the crank-rocker mechanism was the first bicycle drive.

Oscar Egg, a world-hour record holder on upright bikes, used a crank rocker for a streamlined recumbent design. Notice that this is a fixed-gear system where the vehicle motion prevents the pedals from stopping at their dead spots.

And the prolific Gary Hale produces his Glider which employs a crank-rocker.

And the crank rocker is still used to propel most children’s kiddie cars.

Referring to the crank-rocker diagram again, if the pedals are located at point A, they will travel in a circle. If they are located at point B, they will travel in a large arc. If the pedals are attached to the connecting rod, at point C, they will travel through a hybrid of the circle and the arc, an elongated teardrop. These coupler curves have the advantage that the pedal continues to move at the ends of the stroke conserving some of the kinetic energy of the moving limbs. The downside of locating pedals on the connecting rod is the pedals are connected to the frame through two pivotal joints instead of one. This can result in more flexible connection (read sloppy) than a connection through only one joint.

Another oscillating treadle mechanism is a rocking slider. The slider is attached directly to the crank instead of through a connecting rod. To compensate for the transverse motion of the crank, the slider must rotate about its sliding point.

 The K drive, nicknamed because Miles Kingsbury used it on one of his streamliners, is derived from an elliptical trammel. The mechanism can produce a straight pedal path but as configured here it produced a long-thin ellipse. The pedal path produced by this configuration is very similar to that employed in the Beastie.

The other drive mechanism that will be discussed is the constant-torque treadle.

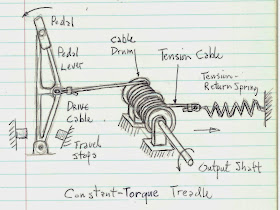
Unlike the oscillating treadle, the ratio of input lever speed to output shaft speed is constant (and as a result, so is the torque). There is a one-way clutch located in the cable drum which allows the input lever to return to the beginning of stroke without reversing the motion of the output shaft. Additional stops must be inserted to limit the input link travel. The ratio of input link motion to output shaft motion can be adjusted by changing the position that the cable attaches to the input lever. This is one big advantage of the CTT; it can incorporate a very simple means to achieve multiple gearing. Some form of return device, usually a spring, must be used to reverse the input link motion at the end of travel.

The CTT is the mechanism most often reinvented by those who would improve the design of the bicycle propulsion mechanism. It is also has been the most prevalent drive system after the rotary crank. It was used on the American Star pre-safety bicycle in the late 1800’s. Paul De Vivie, aka Velocio, the father of the derailleur, experimented with CTTs in the early 1900's. Below is one of his own designs. Depending on where you placed you foot on the treadles, you could vary the effective gear ratio of the drive. A cable connected from one treadle to the other insured that the non-driving treadle moved up while the driving treadle moved down.

 You can still find numerous prototypes today. Steve Ball’s Dragonfly used a modified version of the constant-torque treadle, as did the Pedicar.

There are several reasons why a person designing a human-powered vehicle (HPV) would use a pseudo-linear pedaling motion.

1.       There is interference between the pedals and the steered wheel with circular pedaling motion.

W. D. Lydiard used a rocking-slider mechanism to reduce pedal-steered wheel interference on his entry for D. G. Wilson’s 1968 Human-powered-vehicle design competition, the Bicar. The picture is from the first edition of Bicycling Science by Witt & Wilson.

I experimented with a crank-rocker mechanism in an attempt to reduce pedal-steered wheel interference in my EcoVia commuter trike design.

http://lefthandedcyclist.blogspot.com/2012/09/transcending-pedicar-ecovia-part-2.html

I employed a two sided pedal in this design. The outboard side of the pedal holds the rocker link that supports the pedal. In this location it is spaced wide enough to clear the turning wheel. The inboard side of the pedal holds the connecting rod which is located above the wheel and includes a bend to clear the wheel. This is my interpretation of D.G. Wilson’s crank-rocker concept sketch for a recumbent bicycle.

2.       The foot and knee moving through a pseudo-linear motion take up less volume than circular pedaling.

A classic use of linear motion for this reason is in the Pressodyne streamliner form the late 1970’s. The article is from the Spring 1980 issue of Human Power.

Here are a few highlights relevant to the current discussion. The pedal motion was truly linear using rollers to support the pedal arms. The stilts-version of the Pressodyne used cables that connected the pedals to one-way clutches. This was a constant-torque treadle approach but no efficient means of limiting pedal travel was provided and the pedals crashed into the stops. The three-wheeled version used a crank-slider approach which was much smoother. The smoothness was also due to the fact that there was also no freewheel in the system (fixed gear). So, when the vehicle moved the pedals moved and there was no issue with dead spots in the motion.

The shape of the Pressodyne was not far of the mark for the optimal streamliner shape. Notice the similarity with probably the epitome of streamliner design, the Varna Tempest. The tempest required a bigger nose to house the circular pedaling but had a smaller canopy.

And reducing swept volume of the leg and foot is undoubted the reason Obree employed a teardrop-pedal path in his Beastie.

3.       The linear drive is simpler that a pair of cranks, a chain and two sprockets.

The Mergamobile was a pretty simple approach as was the 1921 J-Rad. One used the different pedal locations to obtain three different gear ratios. Both design use constant-torque treadles.

4.       The linear drive is more efficient than circular pedaling motion.

The constant-torque treadle is the most popular design proposed for improving the efficiency of bicycle propulsion

.

The most publicized use of a constant-torque treadle was in the 1973 Pedicar.

http://lefthandedcyclist.blogspot.com/2012/04/pedicar-technology.html

Trevor Harris, a race car designer and designer of the iconoclastic Can Am Shadow produced the Harris Vertical in the mid 1970’s.

The Alenax Trans-bar bicycle was commercially produced in the 1980’s.

The Alenax was an almost a direct copy of the Svea manufactured in Sweden in the late 1890’s. Paul de Vivie, Velocio, the pioneer cyclo touriste, supposedly experimented with the Svea in his quest to find the perfect touring bicycle.

Notice both the Harris and the Alenax have adjustable cable-attach positions on their pedal levers for variable gearing and both have synchronization mechanisms to move the pedals in opposition to each other. The Harris uses a rocker linkage and the Alenax uses a cable loop.

When discussing the reinvention of the constant-torque treadle, I can’t help but hear Santayana’s quote “Those that cannot remember the past are condemned to repeat it”. In this case “know the past” is more appropriate. The following optimistic declaration that the bicycle has been greatly improved is a fun foil to discuss the shortcomings of constant-torque treadles

.

http://www.youtube.com/watch?v=rj-esh5DQXQ

It also may be useful for the reader to review the section on Power in the following post.

http://lefthandedcyclist.blogspot.com/2014/03/why-hill-climbing-is-hard-or-efficiency.html

Let us begin with why the constant-torque treadle appears to be more efficient than the rotary crank. Assume the rider exerts a force of F in a straight line with each leg. With a rotary crank the torque that is transferred to the wheel is F*sin(theta) where theta is the crank angle. The average torque over a cycle is 2F/Pi or .64F. So from the start, from a torque standpoint the CTT is 57% more efficient.

Unfortunately there are two factors that prevent this increase in torque from being converted to an increase in power

.

Our linear-motion bicycle salesman states that his drive develops full power from the beginning. That is not true. At the beginning of the pedal stroke, the foot is stopped but the output shaft is moving at full speed. It takes a portion of the pedal stroke for the pedals to catch up to the output shaft and during this catch-up phase no force is being produce and, as a result, no power is produced. Both the Dragonfly and the Harris Vertical incorporated cams to gear up the pedal stroke in the beginning to allow the pedal speed to more quickly match the speed of the output shaft. However the cam must be designed for a specific gear ratio. So on the Harris Vertical, the cam will only be effective for around one gear selection.

Another problem is the pedaling speeds that can be sustained with linear drives are significantly lower than those that can be sustained with a rotary crank. This is due to the kinetic-energy fluctuations of the moving limbs. With linear motion the foot stops at the pedal extremes and the kinetic energy drops to zero. With circular cranks, speeds of 300rpm have been achieved because the kinetic energy is relatively constant.  Since power moves the bike and since power is the product of torque times angular velocity, lower pedal speeds result in lower power levels.

The rider is very diplomatic when asked for his impressions riding the linear bicycle. He says it is much better than the first prototype but he doesn’t say it is better than a regular bicycle.

The linear bicycle riders comments that his leg muscles have gotten bigger riding the linear bicycle is an indication that things have become less efficient as opposed to more efficient. When Paul Dudley White, President Eisenhower’s personal physician and bike advocate, rode the Pedicar, he also noticed that it put more strain on the thigh muscles.

One factor that is inconsequential for light-weight vehicles like bicycles but becomes a problem for heavier commuter vehicles is that with the CTT drive, the vehicle cannot be rolled backward. The one-way clutches lock up going backward causing the input levers to jam against the motion stops. This is the reason the Pedicar incorporated a reverse gear at the cost of a significant increase in complexity of the transmission.

There appears to be a means of accelerating the foot at the beginning of the pedal stroke that remains effective throughout an adjustable gear range. When cams were used above, they were inserted in series with the drive cable. I advocate using springs in parallel with the drive cable.

Assume a synchronizing linkage is used to connect the pedals and move them in opposition.  Springs are located so each pedal compresses the spring as the pedal is pushed forward. The springs exert no force at the beginning of the stroke and exert maximum force at the ends of the stroke. Assume the force at the end of the stroke is 2*F.

The combination of the synchronizer mechanism and the springs results in the force vs. pedal position shown in the first graph. With no external load, the zero-force position for the pedals will be at midstroke. From the beginning of the stroke to midstroke, the springs act to move the pedal forward, accelerating the foot. From midstroke to end of stroke, the springs resist forward motion and add to the force required to propel the vehicle. If the average force required to drive the vehicle is equal to F, then each pedal sees a force vs. displacement curve shown in the second graph. The pedal encounters an increasing force from the beginning to the end of the stroke. Since the leg can exert more force as it extends, this matches the pedal force to the legs ability to generate force.

One approach to determining the spring rate for theses springs is to select them so a resonant condition occurs with the moving leg mass. Let us say the moving leg mass for each leg is ½ the mass of the thigh plus the mass of the shin and the foot. From anthropometric data, that comes to about 13.5% of body weight. With a 170lb. rider that gives a moving mass of 23lb. Let the resonance be at 75rpm or 1.25Hz. That requires a spring rate of approx. 4lb./in. Assume a pedal stroke of 180mm or 7in., then F is 28lb.

28lb at 75rpm and a 14” stroke corresponds to 110W. So at a power level of 110W, the pedal force is zero at the beginning of the stroke and 56lb. at the end of the stroke.  The spring rate could be increased so negative to low forces are encountered at the beginning of the stroke for power levels higher than 110W.

After thinking so much about the Pedicar, I couldn’t resist speculating about a drive-system redesign that would address its shortcomings. I also assumed it would be a banking-three wheeler with front steering. As a result the pedal levers are two-piece with the support link outboard of a two-sided pedal and the input link inboard of the pedal. ( See my crank-rocker design for the EcoVia, above.)

 I have included a synchronizer linkage and accelerator springs to smooth out the pedaling. Instead of the Pedicar’s five speeds covering a range of 6:1, I use a shifting quadrant on the input link that can be rotated over an 8:1 ratio, but a range divided into 21 steps. The 8:1 ratio using 16t freewheels as the one-way clutches required a gear-up mechanism. I incorporated a forward and reverse gear set into that mechanism. Recall that, since the one-way clutches prevent the vehicle from being pushed backward, some means of disengaging the drive or having a reverse gear is necessary to move the vehicle backwards

.

When I stood back and looked at the design, I realized that although it addressed the Pedicar’s design deficiencies, it is probably no-less complicated than the Pedicar’s drive, and no lighter in weight. Since the cost of all-weather human-powered commuter vehicles seems to be the greatest factor preventing their popularity, this would not be a good design approach. An ultra-wide range cassette with a single chainring is cheaper, lighter weight and allows the vehicle to be pushed backwards.

So the next iteration of the EcoVia will pass on the constant-velocity treadle.

There is one circumstance where the constant-torque treadle performs significantly better than conventional circular pedaling is when climbing the very steep hills typically encountered in mountain biking. Outstanding hill climbing performance is mentioned in regard to the American Star of the late 1890s and the Pedicar.

A more detailed explanation of hill-climbing problems associated with conventional circular pedaling can be found in the Kinetic Energy and Cyclic Energy Storage section of the Why Hill Climbing is Hard post.

From the standpoint of power generation efficiency (mechanical power out/oxygen in) producing power in pulses interspaced with rest periods is better that producing power continuously. The extra energy produced during the pulses is used up during the rest periods and this energy is stored in changes in the kinetic energy of the vehicle. If the vehicle speed drops below a certain level, the power cannot remain pulsatile and the rider must produce power around the complete pedal cycle instead of the usual pulses produced from 1 to 5 o’clock in the pedal cycle.

The constant-torque treadle is cadence limited but this is not a problem because the cadences associated with steep hill climbing are low. The dead spots in the pedal cycle are only momentary with the CTT and torque is produced for almost all of the cycle while the foot only moves through its normal force generating range. Adding acceleration springs just improves the performance assisting foot motion at the beginning of the pedal stroke.

Come to think of it, a few of the restored Alenax Trans-bar bikes were sporting mountain-bike tires.

If Graeme Obree had propelled his streamliner with convention circular pedaling, he probably would have gone faster, but he would only have a prone-rider record. I believe the linear-drive speed record is technically more interesting.

Hephaestus     

From the Piaggio MP3 to the Toyota i-Road: The Reemergence of the Man-wide Car

I work for a high-tech aerospace company. You would think with all the techie engineers in the place, there would be some interesting vehicles in the parking lot. Except for one vehicle, all the others are pretty mundane. The exception is a Piaggio MP3 three-wheel leaning scooter. It belongs to one of our technicians and, with more enthusiasm than he may feel is justified, I tell him he is riding the future.

The extra wheel significantly increases stopping performance and the ability to lean allows the MP3 to be controlled when the wheels break free on slippery surfaces. This is opposed  to the vehicle falling over if it had just two wheels. While road testing the new 500cc version of the MP3 LT, a Cycle World reviewer dropped (out-distanced) a rider on a BMW R1200GS on a snow-slicked section of curved Berlin highway, a clear indication of the performance potential of a leaning trike. The LT stands for large track, an acknowledgement of the front wheel spacing being over 650mm. In Europe and the UK, if a trike has a track wider than 650mm, it is consider a car and can be ridden without a cycle license or a helmet. Only an auto driver’s license is required.

By making the MP3-LT controllable on slippery surfaces, Piaggio has taken a huge step forward to producing an all-weather scooter.  And with top speed in excess of 80mph and a fuel economy of 60mpg, is offers an attractive commuting alternative to an auto. It just needs a body and it could be considered an all weather scooter, or in a broader sense, a man-wide vehicle or MWV.

In a University of Michigan sustainability study for 2010, vehicle occupancy was calculated to be 1.55 persons per vehicle. That means that for most of our trips and the majority of vehicles there just one occupant in the auto. It is clear that one person in a four-person vehicle is moving too much mass, pushing too much air, burning too much fuel  and taking up too much space.

Most trips could be accomplished using a vehicle tailored to one person or two persons in tandem, a man-wide car. Since the vehicle is lighter and more aerodynamic (less frontal area), fuel consumption could be significantly reduced. And the smaller vehicle size would allow more vehicles to occupy the same lane width as a normal-width vehicle.

The investigations into MWVs by large auto companies are not new. Honda had its EP-X which seated two.

Volkswagen had its L1 which also seated two.

And general motors had its Lean Machine which only sat one.

But only the Lean Machine approximated the width of a motor cycle, 850mm (33.5”), with its 915mm width. Narrow-track three and four-wheel vehicles risk overturning when cornering. Allowing the vehicle to lean like a motorcycle provides  for dynamic stability  and allows the width to remain narrow without the risk of overturning. The Lean Machine was narrower than these other attempts because it could lean.

http://lefthandedcyclist.blogspot.com/2012/02/drymer-and-varna-lean-forward.html

Now both Toyota and Nissan have MWVs that utilize leaning to reduce the vehicle width. Both are completely electric powered.

The Nissan Land Glider uses four wheels that are articulated allowing the vehicle to lean. At 1100mm width, the Glider is wider than a motorcycle but still significantly narrower than a Smart Car’s 1550mm width. The glider seats two in tandem.

 The Toyota i-Road is also a dual occupant vehicle that is narrower than the Glider at 850mm, mostly due to the layout (like the Lean Machine) where the single wheel does the steering and thus doesn’t require the width that two-wheel steering does. What is unusual about the i-Road is the single-steered wheel is in the rear. If the instability issues associated with rear-wheel steering can be overcome, (see below),

http://lefthandedcyclist.blogspot.com/2012/01/bucky-and-urbee.html

this layout is ideal for packaging. Because the front wheels incorporate the electric-drive motors there is room between them for the driver while maintaining minimum vehicle width and the steered wheel fits easily in the width of the vehicle. 

I attempted to use this layout for the initial design approach of my EcoVia commuter trike, but could not come up with a mechanism for stable control of the steering and leaning that functioned at anything  but low speeds.

http://lefthandedcyclist.blogspot.com/2012_08_01_archive.html

Fortunately, the i-Road can utilize active electronic control to insure stability. The i-Road’s top speed is less than 40mph so it is not suited for highway use. What is encouraging is that the project has graduated to the consumer test phase where 20 Japanese drivers will get to evaluate the i-Road under real-world driving conditions.

Probably the most unusual approach to developing a MWV is the C1 from Lit Motors. It uses two gyroscopes to balance the two wheel vehicle. Gyro-stabilized two-wheel vehicles have been around since the dawn of the automobile, but in this case, since the vehicle is all electric, power is available to keep the gyros running temporarily even when the drive motor is turned off. It also features twin retractable support legs that hold the vehicle up when permanently stopped. The amount of balance torque generated by the gyros is impressive and will insure the vehicle stays upright during collisions. It will seat two people. Since it has only two wheels, it will require a motorcycle license to drive.

The i-Road and the C1 are essentially all-weather motorcycles, but for the increased cost, buyers will require significantly more crash protection than your average motorcycle. Providing this will require some creative use of materials and structures to prevent significantly increasing size or weight.

If MWVs become numerous, they may cause changes in highway infrastructure. Single wide highway lanes could be turned into two narrow lanes, and therefore improve traffic throughput. This would require recognition that the smaller vehicles merit special consideration which may be a difficult sell to the general public.

I rented an original Honda Insight when my car was being serviced. Since the car was more narrow that what I had been used to, sitting in the car in my driveway I could imagine the vehicle was only one-seat wide. As long as I am warm and dry and can safely maintain highway speeds, I could live with a vehicle like that.

Hopefully, in the not too distant future, there may be mature MWVs parked in the lot where I work. Maybe one will be mine.

Hephaestus

The Sinclair C5 to the Organic Transit Elf: Pedalectric Identity Crisis

The Sinclair C5

The Organic Transit Elf

One would think if George Georgeiv’s Varna Tempest could cover a distance of over 56miles in one hour, that it would be a straight forward process to design a commuter vehicle that could travel at half that speed, a vehicle that could keep up with urban traffic while only requiring about 200Watts of mechanical power. To date, this has proven to be more difficult than I would have expected, partly due to the increased requirements that go along with comfortable and safe commuting.

The first decision that designers must address is predominately where the vehicle will be ridden.

If it is mostly on bike paths, the vehicle can be considered an all-weather electric bicycle, or AWEB. (I use the term bicycle to embrace the most common embodiment of a pedaled vehicle. It will more likely be a tricycle.)

It takes more than adding a third wheel, a motor and a body to produce a fully functional AWEB.

 The main criteria is to keep the vehicle narrow enough to fit within bike lanes and keep it high enough to be visible to other cyclists and autos when it is ridden on shared roadways. For the bike lanes I use, the width needs to be less than about 33 inches.  (The width of a motorcycle is considered to be about 33 inches). If the vehicle is to be stable on slippery road surfaces it will require three wheels and if it is to have reasonable corning speeds without tipping over, it must be a leaning tricycle.

http://lefthandedcyclist.blogspot.com/2012/02/drymer-and-varna-lean-forward.html

Most locations have speed limits for electric bicycles which limit their effectiveness in challenging cars for commuting purposes. In the US, the electric bicycle speed limit is 20mph.

If it is to be ridden where it shares the traffic lanes with autos it can be considered a pedal-electric car or PEC.  A PEC needs to be visible and able to keep up with traffic to not cause congestion. Where I live that means that it needs a top speed of 40mph.

In addition, for adequate traction on slippery road surfaces, more then 50% of the vehicle weight should be on the driving wheels.

The Drymer discussed in the post listed above comes very close to meeting all the requirements of an AWEB. The Cyclodyne discussed later came very close to meeting all the requirements of a PEC without an electric assist

.

In 1985 the British electronics industrialist Sir Clive Sinclair decided to mass produce one of the first pedalectric vehicles. More than just an electric bicycle, it had three wheels and a partial faring.  The pedals drove one rear wheel and an electric motor drove the other. Lotus Cars developed a flexible chassis in lieu of a suspension and Polymotor of Italy developed a motor with an integrated gear-reduction. To take advantage of riding the C5 without a license, the top speed was limited to 15mph.

 Automotive Engineering titled its May 1985 article “Motor Assisted Trike Presages Electric Cars.” For all the media hype and large financial investment in the project, 12million pounds, the result was an abysmal failure.

 Here is a list of the more obvious failings:

   1.        It had only one pedal speed.

   2.       The pedal cranks were much shorter than normal.

   3.       The pedal-seat distance couldn’t be adjusted.

   4.       It was too low to be visible in traffic.

   5.       It had poor weather protection.

   6.       It didn’t have enough electric power to get uphills.

   7.       The front wheel was too small.

Below is a picture of a tall rider, Automotive Engineering’s European Editor Scott, wedged into the vehicle.

Clearly there was no input from cyclists on the pedal drive or there would have been multiple gears and an adjustable seat-to-pedal distance. The pedal portion of the vehicle was merely window dressing.

The height issue was addressed by adding a tubular loop in the rear that could hold flags or reflectors.

The inadequate weather protection was addressed by adding a rain suit and waterproof side covers. (Anyone that has ridden a recumbent in the rain will see that this rider will develop a puddle in his lap!)

There were a few features that were to be commended. The overall design had an attractive, streamlined esthetic, in some part due to the delta configuration (one-front wheel, two rear wheels), which allowed the steered front wheel to comfortably enclosed by the nose of the vehicle. And having the handlebars beneath the seat proved a comfortable location.

In the end there were 17000 vehicles sold, but many owners abandoned the pedals and used electric power only. Although it aspired to be an AWEB, the C5 ended up being little more than a recumbent electric scooter.

Skip ahead 19 years to the Elf from Organic Transit of Durham, N.C. The Elf is a semi-enclosed electric tricycle using the tadpole configuration (two front wheels, one rear wheel). The pedals and the electric motor drive the rear wheel. It is a noticeable improvement over the C5. It has much better weather protection. The seat-to-pedal distance can be adjusted and it has multiple speeds. Below is a picture of an Elf chassis being assembled. The seat slides on the two-horizontal rails between the front and rear wheels.

Everything looks promising until we check the vehicle width, which at 48 inches is too wide to fit within most bike lanes. In addition, the rear wheel appears to support less than 1/3^rd of the vehicle’s weight, so traction in snow will be a problem. (The Organic Transit site shows a pretty picture of an Elf in on a snowy road.) So the vehicle width prevents it from being a viable candidate for an AWEB. On the other hand, since the speed is limited to 20mph, it is not a candidate for a PEC either.

The people at Organic Transit are working on the next generation of the Elf. So one suggestion for a simple improvement is to go from the 26 inch dia. wheels to the more standard (for human-powered vehicles) 20 inch dia. wheels. These are more electric-motor friendly since they rotate faster. They also take up less space, so volumes for turning and fenders can be smaller, leading to a more streamlined design. Another simple improvement is to have only one door (like the Pedicar). This provides for a more continuous structure for the body and better weather protection.

If they are interested in adding leaning to their design, it would benefit them to take a closer look at how the Drymer people incorporated leaning into their trike design.

Because the Drymer leans, the c.g. of the vehicle can be shifted toward the rear wheel without concern for tipping during cornering. As a result, traction for the driving wheel is improved and suspension on only the rear wheel is very effective.

The Organic Transit people also have a utility trike on the drawing board called the Truckit. The Truckit uses a delta configuration for the wheel locations with pedals driving the front wheel.

 A more compact and streamlined concept for a delta-configuration velo truck, based on the EcoVia leaning-trike, is shown below.

http://lefthandedcyclist.blogspot.com/2012_09_01_archive.html

The pedals drive a central driveshaft and the two leaning wheels are chain driven off that shaft.

 

The truck is 108 inches long, 33 inches wide, 57 inches high and has a cargo capacity of over 25 cubic feet. The leaning can be locked up for loading and low speed operation. The pedals drive both rear wheels and the motor drives both rear wheels through twin ratchets that act like a posi-traction differential. This produces excellent performance on slippery surfaces.

Had the Cyclodyne from the 1980’s incorporated an electric drive to supplement the pedal drive, it would have been the first successful PEC.

Even though it had a pedal-powered cruise speed of 30mph, it wasn’t quite fast enough to keep up with traffic, which it needed to do because it was almost as wide as an Elf. The addition of electric assist could have easily increased its top speed to over 40mph.

The Cyclodyne drove and steered both front wheels providing excellent all-weather traction. It would have been straightforward to integrate an electric motor into that drive.

So in conclusion, I believe that AWEBs, operating on most bikeways will have to use the leaning-trike configuration.

Bridgestone seems to reinforce this point by joining  the ranks of the AWEB's with their own version of a Drymer-like leaning trike.

For the less common PECs, leaning is not a requirement, since they will be able to keep up with cars and can therefore be wider. That being said, being able to lean makes the vehicle narrower and more aerodynamic. And this makes it more efficient. 

Automakers are again looking at tandem-seating two-passenger vehicles for fuel economy and they are also incorporating leaning to reduce the vehicle width. More on these man-wide vehicles in the next post.

Hephaestus