Why designers select three wheels for vehicles:
Compared to their four-wheel cousins, you see very few three
wheel automobiles. I think that the basic reason for this is that, for layouts
where all three wheels are equally loaded, and the vehicle tracks (width over
the paired wheels) are the same, quad wheelers can corner at a 50% higher
accelerations than trikes. Thus trikes need to be about 50% wider than quad
wheelers for comparable tipping resistance.
So why is there continued interest in trikes by progressive
vehicle designers? One reason it that tricycles are less regulated that quads.
If light enough (less than 1500 lb. in the US?) the vehicles are considered
motorcycles. And if the power is low enough, they can be considered mopeds. And
if slow enough (less than 20mph in the US) they can be considered electric
bicycles and have access to bicycle paths.
Another reason trikes are popular platform for new vehicle
concepts is that they can be simpler than quads. For tadpole layouts (two
wheels front, one behind) they can use motorcycle or bicycle transmissions to
drive the rear wheel. For delta layouts (one wheel front, two behind) they can
use motorcycle or bicycle fork steering. And delta trikes can be more
aerodynamic than quads.
A three-wheel pedal-electric vehicle:
So let’s look at a
hypothetical pedal-powered commuter vehicle with electric assist. We make it a
three-wheeler to take advantage of the reduced vehicle regulations. We want
car-type seating with pedals about 10” below the seat, so we choose the tadpole
layout. The pedals easily fit between the two front wheels.
We want a rollover resistance of at least one gee. The
rollover gee limit for static vehicles is approx.
Gees=w/2*hcg
Where w is the track width (distance between paired wheels)
and hcg is the height of the center-of-gravity off the ground. For tricycles,
where the weight is equally distributed over the three wheels, w is approx. 2/3
the spacing between the wheels.
Automobiles regularly have rollover resistances in excess of one gee. And some sports cars can approach two gees or more.
For the one gee roll over resistance and a hcg of 16", we will need a track of about 48".
.
Both the Elf from Organic Transit and
the Velocar from VeloMetro are actual examples of our hypothetical tricycle layout vehicle. Not surprisingly, they both have tracks of 48"
The Elf is shown below.
The proof-of-concept for the Velocar is shown below.
If a track of 48” is too wide for the paths the vehicle is
to use, there is an unconventional trike layout that can be employed. I call it
the Coventry-trike layout in honor of James Starley’s Coventry Rotary tricycle
of the 1880s.
A modern version of the design would probably use equal
sized wheels, all cantilevered for ease of removal and tire replacement. One advantage of this approach is that, if the
drive wheel is located along the c.g. in the side-to-side direction, 50% of the
vehicle weight in on the drive wheel as opposed to the conventional tadpole
layout which only has about 33%.
One downside of this layout is that the trike
would tip forward during hard braking. Tipping could be prevented, however, by
having a caster near the ground opposite the front steering wheel and in front
of the driving wheel. This caster could be frictionally loaded so when the
trike tipped forward and the castor contacted the ground it contributed to
braking.
The most complicated method of reducing the width of the
trike, but maintaining its rollover resistance is to allow it to lean. The
designers at VeloMetro considered making their Velocar a leaning trike, but
since their business model was to rent their trikes to people for short trips,
the associated learning curve would have been impractical. Leaning trikes have
all the issues of recumbent bicycles, plus more if the vehicle is in and
enclosed body. See below,
For bicycles and free-leaning trikes,
Gees=tan
(alpha)
Where alpha is the lean angle from vertical. For one gee of
rollover resistance the lean angle is 45deg, which is quite a bit of leaning,
and is to the state when the tire contact with the ground could be on the
sidewalls, not the best for adhesion.
If properly implemented, however, leaning trikes can develop
more rollover resistance than just the bicycle-lean effect.
Since I have spent a good deal of time working with the
delta trike layout, let us examine another hypothetical vehicle. It has a width
of 30” and a track of 26”, a wheelbase of 48” and a c.g. height of 24”. It can
lean 30deg. from vertical.
Below are diagrams of this trike seen from the top and the
back. The trike is fully leaned over.
There are four rollover accelerations associated with this
design. Two are common and the other two are associated with leaning trikes.
(Lean locks are discussed in more depth in the post above.)
The first acceleration is when the trike is locked
(lean-locked) in its upright position. This upright–locked acceleration is 8.5”
(dim a. in figure 1. from the upright c.g. to the tipping line A-B) divided by
24” (the c.g. height) or .35gees.
The second acceleration is due to leaning (like a bicycle).
This free-leaning acceleration is tan(30deg) or .58 gees.
A leaning trike can corner harder than a bicycle for a given
lean angle because the wheel opposite the lean direction increases the distance
from the c.g. to the line of tipping This acceleration is when the trike is
fully leaned over and the lean-lock is engaged. This lean-plus acceleration is
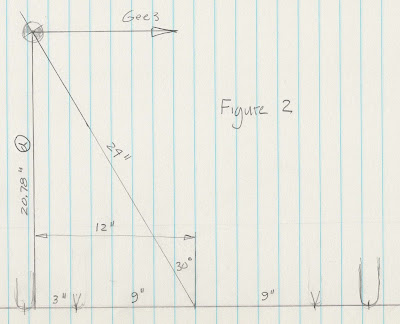
20” (dim b in fig.1 the distance from the c.g. to the tipping line A-B) divided
by 20.78 (dim d in figure 2). The lean-plus acceleration is .96 gees, almost .4
gees greater than the free-leaning acceleration.
The last acceleration is associated with the tendency of the
trike in the leaned-over but lean-locked state to tip in the opposite
direction. This counter-tipping acceleration is 3.5” (dim c in fig 1, the
distance the c.g. overhangs the tipping line A-C) divided by 20.78 (dim d in
figure 2) or .17 gees.
Sounds confusing, doesn’t it.
To try and make things clearer, let’s have our rider, from
the Mango tipping video above, ride our trike through a progressively
tightening turn. The rider gets into the delta trike with leaning locked
upright. The rider begins to make a turn. When the acceleration of the turn
reaches .35 gees, the lean lock must be released to prevent tipping. The turn gets tighter and the
rider leans into the turn. As the turn gets to .58 gees the rider is at the
lean limit. If the turn gets tighter the rider will not be able to maintain the
lean and will be pulled upright. However, if the lean lock is again engaged at maximum
lean, the rider can corner with an extra .38 gees without tipping.
Now even though the trike is locked up with the c.g.
outboard of the left tip line (A-C) the trike won’t tip over as long as the
turn is at least .17 gees, the counter-tipping acceleration. The acceleration
of the turn must drop from the .96 gee max to .17 gees before the lean-lock
needs to be released and free leaning can resume. This is plenty of time to do
this.
The requirement to continually engage and disengage the lean
lock may be too much of a complication for a human-powered commuter vehicle.
But for powered vehicles that can employ automatic lean actuators based on
vehicle accelerations, this would all be transparent to the user. The driver
would just steer and the onboard computer would determine the appropriate
amount of lean.
Hephaestus






Hi Hephaetstus- We met on the Sammamish Trail the other day, me with the Vision recumbent. Drop a line if you want to talk electric assist HPVs. I enjoyed the blog.
ReplyDeleteKen
mycatbites(at)gmail.com
Thank you so much for such an informative piece of information :)
ReplyDeleteIf anyone interested similar one's have a look here
Mountainbikelabs
Thanks